光走直线?大家都能懂的量子电动力学

1/11
费曼(Richard Feynman)是获得诺贝尔奖的物理学家中少有愿意和公众接触,并擅长传播科学的大科学家,这和他性格极其外向有关,费曼曾经的同事这样评论:“作为同事,如果他邀请你去脱衣舞夜总会,那这表明费曼是很认真的把你当做一个物理学家看待了。”
1961年加州理工学院物理系招生状况已经很不理想了,为了改善这种情况他们请来了费曼,知道他善于演讲,也预计在授课中会出彩,所以做了非常充分的准备,包括有人专门录音,有人专门拍照记录课堂笔记。费曼接受了2年的教学工作,学生是入学新生,大一到大三。很难想象一个诺贝尔奖获得者会愿意花大量时间为新生讲课,但费曼的兴趣也在于此。2年后他讲课的内容被整理成册,这就是到现在依然在世界各大高校物理系必选的《费曼物理讲义》。
今天介绍的一些想法就来自于费曼的思考,我们先不把它复杂化,从最简单的光开始说起吧。
2/11
初二物理课中老师讲到光,要记住2点
1、均匀同种介质中光沿直线传播
2、遇见镜面时入射角等于反射角
除此之外还有一些折射角入射角的关系,也完全是按公理给出,没有解释原因,如果追问为什么,老师就会回答,本来就是这样。
但在费曼的体系中没有这样先验式的内容,取而代之的是一些更加基本的假设。当然你不能问这些假设是怎么来的,因为费曼也不知道,他只知道这样假设后,一切我们可以观测到的电磁波、电磁波与物质的相互作用都可以描述得非常精确,精确到相距150公里远可以用一根针射断一根头发。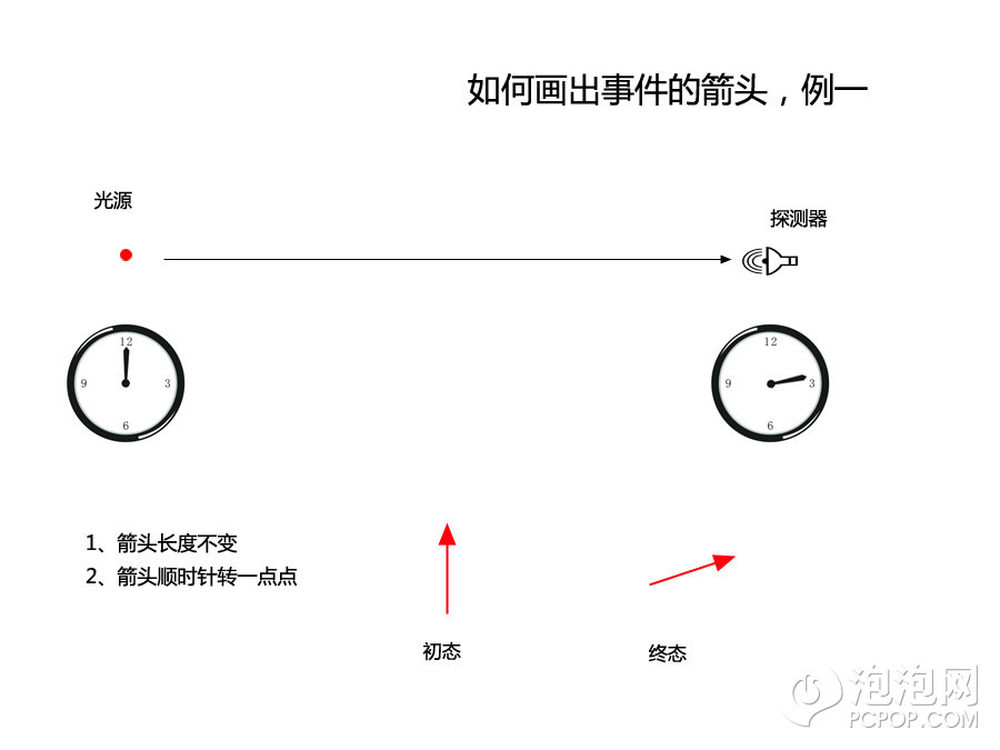
3/11
光从光源出发,直到探测器收到。我们把这当做一个事件。我们先假定这束光并不分散,这样有多少光从光源射出就有多少光被接收器探测到。
我们规定
1、箭头长度的平方代表事件发生的几率
2、箭头的偏转角度代表事件经历的时间,你可以想象成一个飞快旋转的钟表,哪怕经历很短的时间它都会偏转一些角度。(其实箭头转一圈的时间和这光的振动周期一样长)
那么一束光从光源射到探测器用箭头表示时,初态就是一个单位长的箭头,方向任意,我们就用竖直向上作为时间零点,那么经过一段很短的时间后到达探测器,终态的箭头角度就是一个顺时针稍稍偏转的方向。因为所有发出的光都能接收到,所以终态箭头的长度不变。图中画出了初态和终态。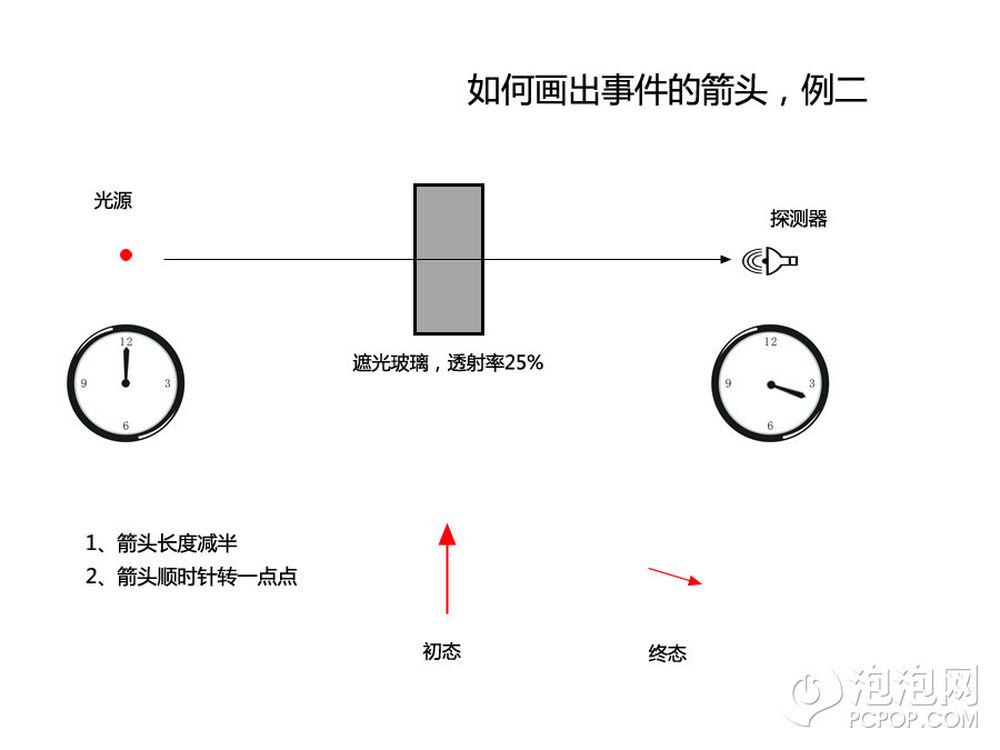
4/11
在第二个例子里我们对第一个例子稍加变化,在光源和接收器之间插入一块遮光玻璃,入射的光线只有25%%能透过玻璃到达探测器。所以终态的箭头不但旋转的角度更大了(因为在其他介质中光速变慢了,所以需要时间较长),而且由于透射25%%所以箭头长度缩短为初态的二分之一(0.5的平方是25%%)。
这个2个例子中只有一个事件,如果事件有多个可能的情况,则事件最终的结果就是把所有可能的事件箭头首位相连后再从第一个事件箭头的尾,到最后一个事件箭头的头连起来形成一个最终的大箭头,这个箭头旋转过的角度就是整个事件历经的时间,这个大箭头的长度的平方就是整个事件得到最终结果的几率。
如果这个例子也看懂的话,下面我们就要好好利用箭头了。
5/11
刚刚我们只是为了介绍箭头如何画才假设光从光源走直线射入探测器,但仔细想想这样做是没有道理的,因为事先没有“光沿直线传播”这个大前提存在,所以我们应当假设光可以沿各种各样的路径到达探测器。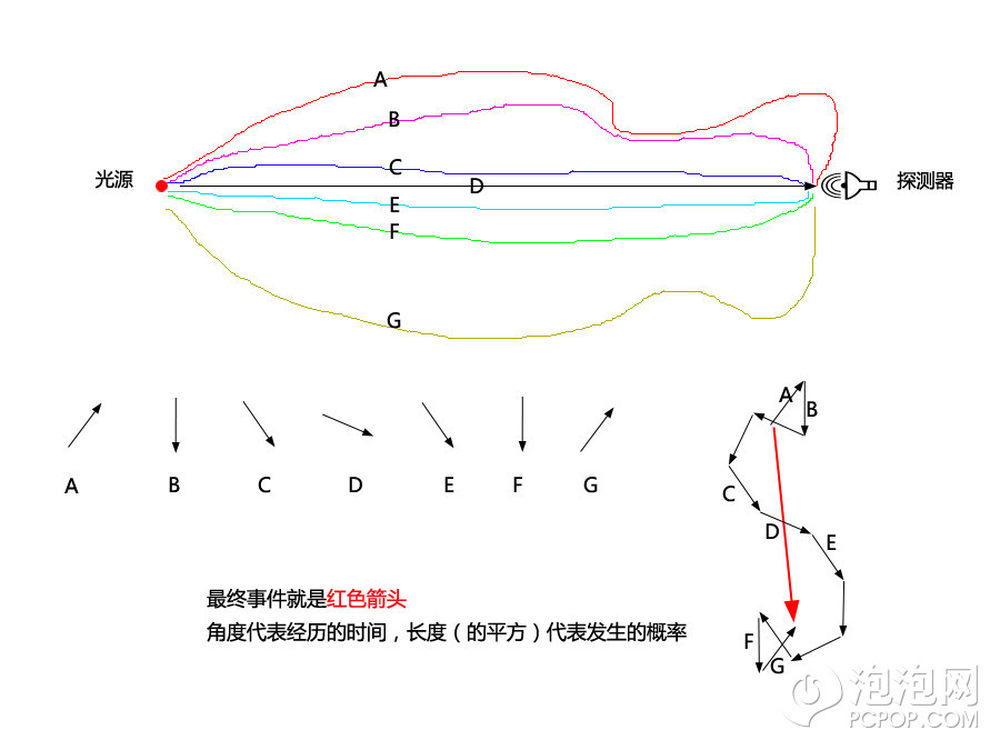
6/11
我一共画出了从光源到探测器间7条路径ABCDEFG,实际路径是无数条的,只是因为画不下了。
我标出了光走每条路径的这个事件的箭头,可以看到他们的长度相同,因为我们没有理由认为某一条路径比其他路径更有可能出现,他们的机会均等。不同之处在于箭头的方向,如果假定光走A路径经历一段时间后到达探测器后箭头向右上方,那么B路径因为比A更接近直线所以需要的时间比A要明显少,所以AB两个箭头角度变化大。
CDE这3个箭头的角度变化远没有AB的差异那么大,这是因为这3条路径的长度相仿,所以经历的时间也不会相差太多。
如果我们再把A到G之间的路径再多补充一些,就能画出右下角的图,一共12个箭头,比7条路径多,这是因为我图中画不下那么多了。
最终从光源出发的光在探测器接收到这个事件的就用红色箭头描述,可以看到离中心线较远的那些路径所代表的箭头如果首尾相很容易出现原地画圈的情况。这等同于这些路径对“光源发出探测器接收到”这个事的出现几乎无贡献。而促成此件事发生的大部分贡献来自于那些箭头方向大致朝下的黑箭头。也就是和红色大箭头方向差不多的那些黑色箭头。
如果我们用箭头来描述光的话,光并不真只沿着一条直线前进,它在行进时占用了直线周围的一束小小的空间。离这条直线远的地方光线总因为箭头原地打转而几率相消。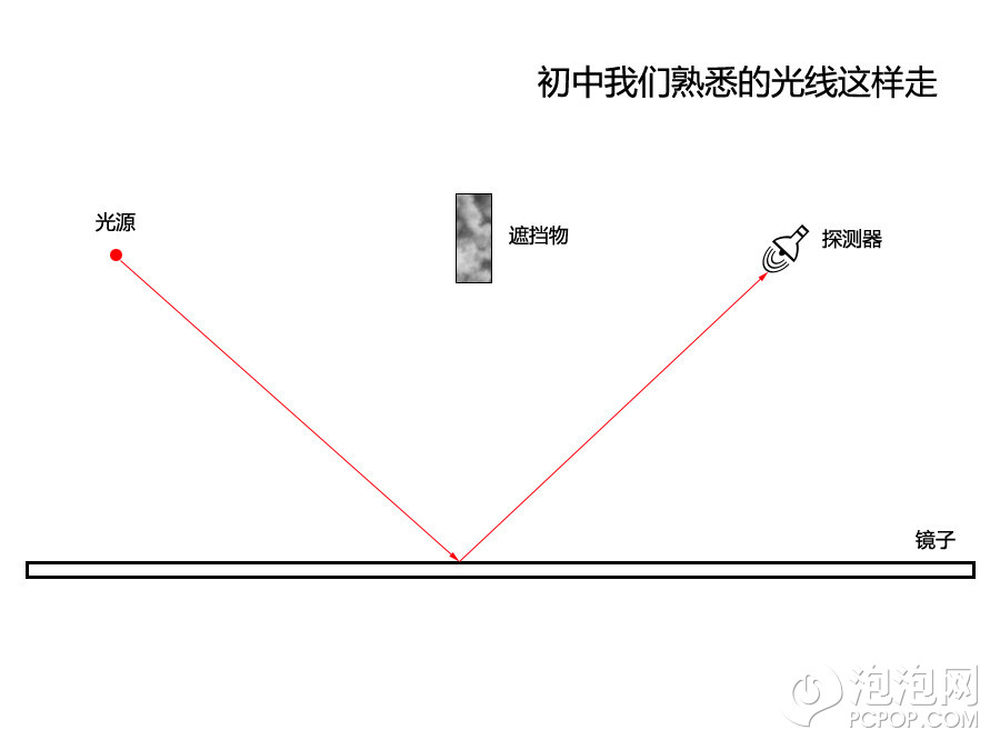
7/11
初中学的镜面反射我们按图中这样画。如果用新观点去理解镜面反射呢,那首先要认为光从镜面任意处都可以反射到探测器中,然后我们把所有可能的事件箭头首尾相连,就是最终的光源发出的光在探测器接收到的几率。请看下图。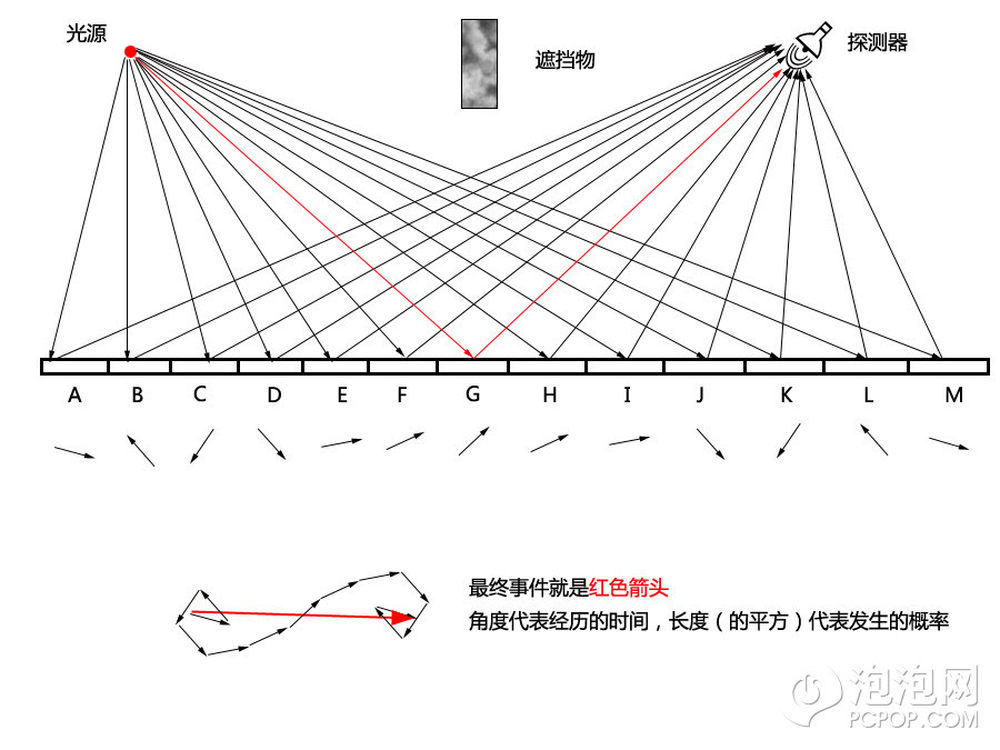
8/11
我一共画了13种反射的路径,说实话,谁有好的工具可以一键生成啊,这么一根根的画费了我一小时。每条路径的小箭头我都画在对应的字母下面了。
同样理由我们会发现在镜子最左侧和最右侧箭头对最终事件发生的贡献几乎没有,因为他们和周遭路径的箭头首尾相连后在原地打转转,而对镜面反射事件贡献最多的是那些方向大致和红色大箭头相仿的黑色箭头(EFGHI)。
所以可以这样理解:要发生镜面反射镜子必须要有足够的尺寸,如果镜子小到无法容纳邻近的路径通过,那么在探测器处收到光子的几率将大大减少。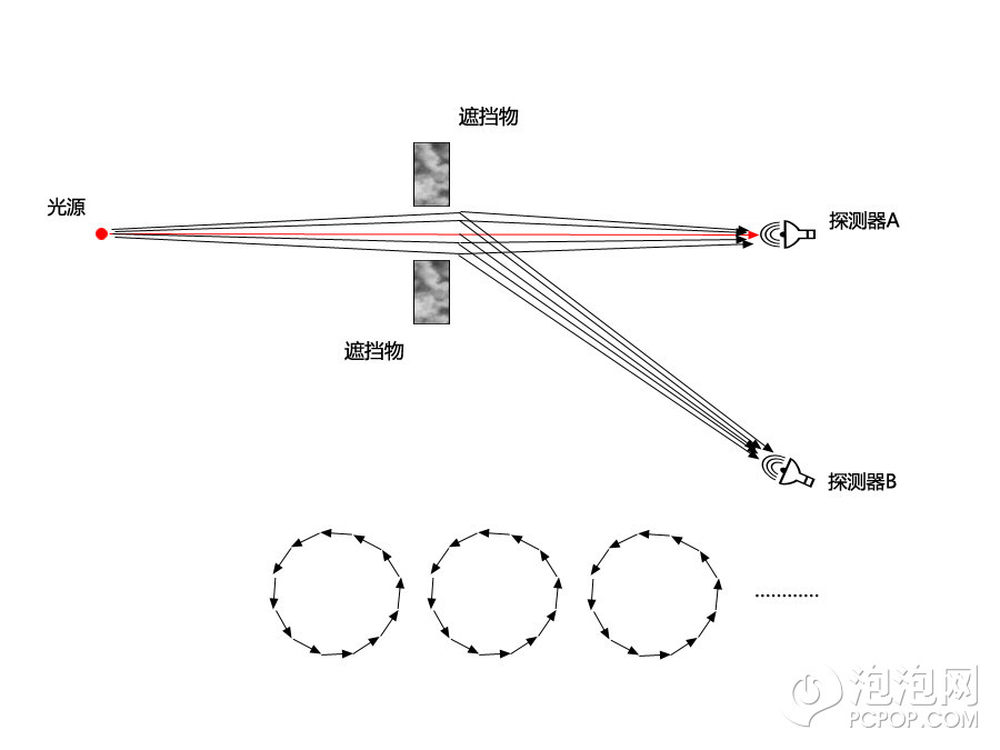
9/11
我们最后看个光穿过狭缝的例子,两个遮挡物间有道狭窄的缝隙,对面有探测器A,一般来说在探测器B的位置你是接收不到多少光的。但这并不是因为光沿直线传播到A,而不经过B。运用刚才介绍的原理我们能分析出原因。
我随手画了一些光从光源经过狭缝最后被探测器B接收到的可能路径,你会发现他们因路程差导致了明显的时间差,而时间差会导致相邻的路径小箭头最终拼接成一个圆圈。从狭缝的上沿开始往下扫,所有可能的路径中,每往下扫一段距离,若干传播路径所代表的箭头首尾相连就会形成一个闭合的圆圈,再往下扫就会绕第二圈,最终扫到狭缝下沿处时无数的箭头只是在绕圈圈。绕圈意味着首尾相连后最终事件的箭头长度为零,也就是在B处发现光的几率为零。
严格来说最终事件的箭头长度并不一定会是零,因为只要箭头在绕最后一圈时没有转满360度那么从出发到结尾连起来的箭头至少有一点点长度,这个长度的平方就代表了我们在B处看到光的几率。但这个箭头的长度和无数个箭头朝大致同一方向组成的大箭头长度相比要短非常多,平方后差距就更大。所以光在穿过比较宽的狭缝时B处几乎看不到光。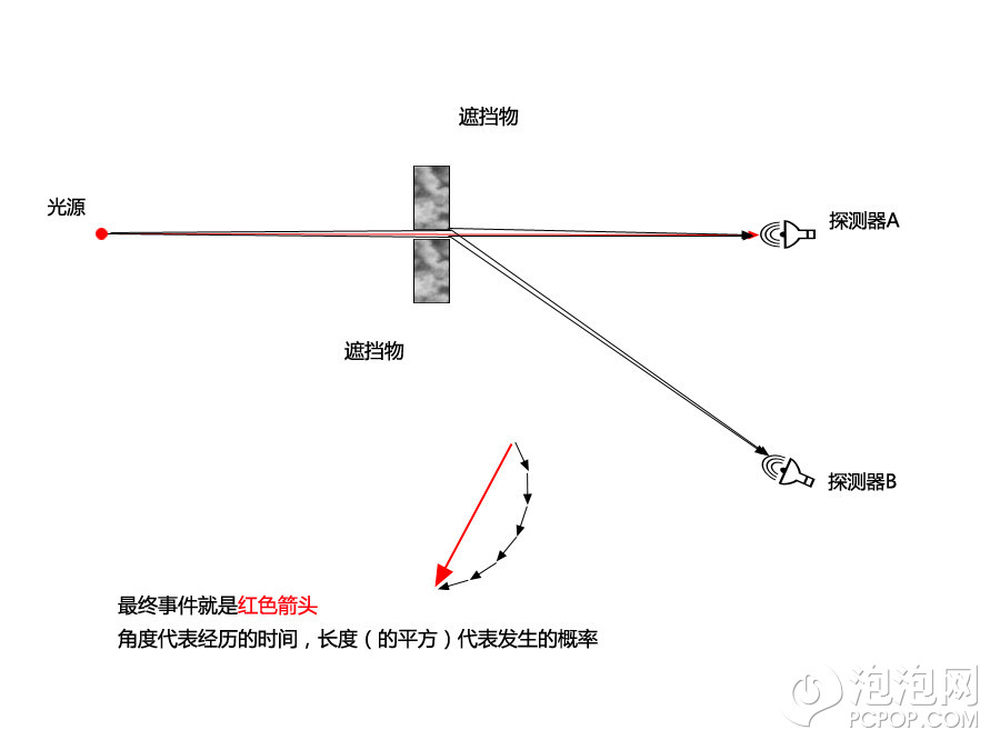
10/11
如果狭缝很窄,窄到光出发后经狭缝上沿到探测器B的距离,和经狭缝下沿到探测器的距离大致相当的话,那这两个事件的箭头角度差就不会太大,上下沿之间的路径虽有无数条,他们偏转的角度更小,所有可能性叠加在一起,箭头首尾相连后并不能绕成一个圈圈,而且大部分箭头的指向性趋于一致,所以最终得到的终态大箭头长度很可观,于是当狭缝很小时在B观测到光的几率就非常大,在狭缝很小时探测器A处也同样有很大几率看到光。
11/11
编辑总结:
光沿直线传播、入射角等于反射角等等我们熟悉的关于光内容实际上只是对光现象的一种粗略近似的描述。而当前的这些描述所涉及的理论虽然不能说完美,但起码可以准确预测、描述除引力与核力以外所有现象。它的内容远远不止于此,如果大家感兴趣,下一篇我会从电子与光子的相互作用中找出一些有意思的内容发出来。
虽然描述很粗糙,不严格,但也让人震撼,费曼需要拥有很深的洞察力才能构建起这套理论。而大家今天了解到的一部分概念就是量子电动力学中一点点内容。
---------------------------------------------------------------------
最后把《费曼物理学讲义》共3册,推荐给大家,200.6元。>>京东购买链接